奇函数与偶函数相乘的结果是什么？

在数学的浩瀚宇宙中，函数如星辰般璀璨，它们以各种形态和性质交织出一幅幅壮丽的画卷。今天，我们要探索的是一场特别的邂逅——奇函数与偶函数的乘积，它们相遇时会产生怎样的奇妙结果呢？

奇函数：数学界的神秘侠客

首先，让我们来揭开奇函数的神秘面纱。奇函数，就像武侠小说中的侠客，行踪不定，但总有一些不变的规律可循。它的定义很简单：如果对于函数f(x)，满足f(-x)=-f(x)，那么它就是一个奇函数。这意味着，当自变量x取反时，函数值也会取反。奇函数关于原点对称，它的图像仿佛是在坐标轴上翩翩起舞的蝴蝶，轻盈而优雅。

偶函数：数学花园中的优雅公主

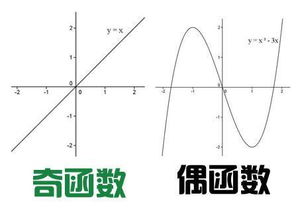
而偶函数，则是数学花园中的一位优雅公主。它的定义同样简洁明了：如果对于函数g(x)，满足g(-x)=g(x)，那么它就是一个偶函数。偶函数的图像关于y轴对称，仿佛是一面镜子，映照出函数值的恒等不变。偶函数就像是一位温婉的公主，静静地守候在数学的殿堂中，等待着与奇函数的奇妙相遇。

奇函数乘以偶函数：奇妙的化学反应

当奇函数与偶函数相遇时，会发生怎样的化学反应呢？让我们通过一个简单的例子来揭示这个秘密。

假设我们有一个奇函数f(x)=x和一个偶函数g(x)=x^2。它们的乘积h(x)就是f(x)*g(x)=x*x^2=x^3。现在，让我们来分析一下h(x)的性质。

当我们将x替换为-x时，h(-x)=(-x)*(-x)^2=(-x)*x^2=-x^3。注意到这里的结果与h(x)正好相反，即h(-x)=-h(x)。这意味着，奇函数与偶函数的乘积其实是一个新的奇函数！

这个发现不禁让我们惊叹于数学世界的奇妙与和谐。就像武侠小说中的侠客与公主相遇，产生了一段传奇的故事一样，奇函数与偶函数的乘积也在数学界留下了浓墨重彩的一笔。

探索不止，数学之美无穷

通过今天的探索，我们不仅了解了奇函数与偶函数的基本性质，还发现了它们相乘时的奇妙规律。数学的世界就像是一座宝藏库，等待着我们去挖掘和发现。每一次的探索都可能带来意想不到的惊喜和收获。

所以，让我们一起继续在数学的世界里遨游吧！去发现更多的奥秘和美丽。因为，在这个充满奇迹和可能性的世界里，数学的魅力永远无穷无尽。